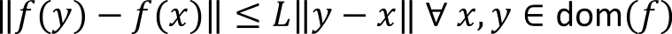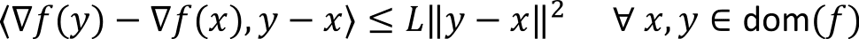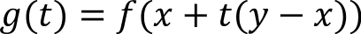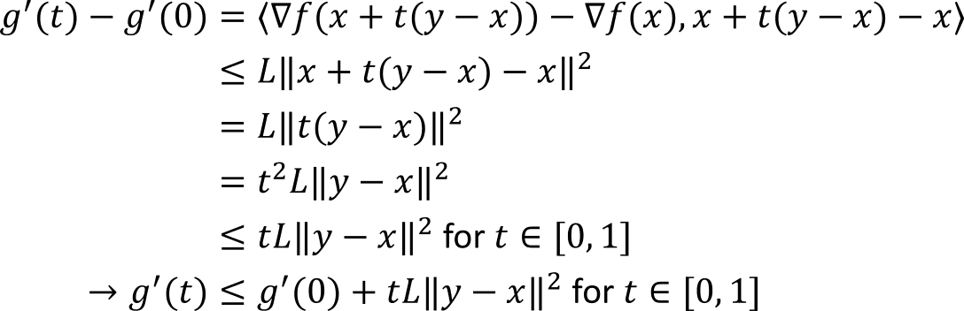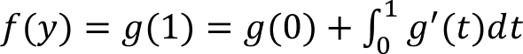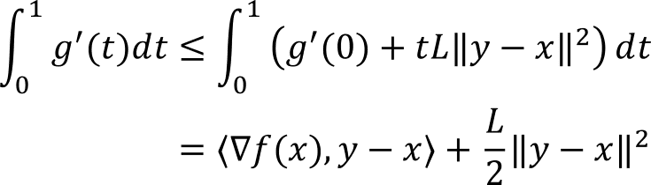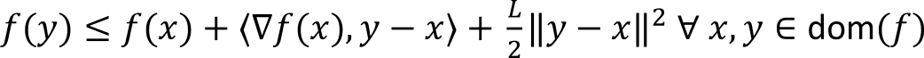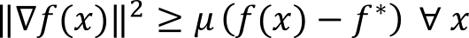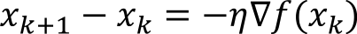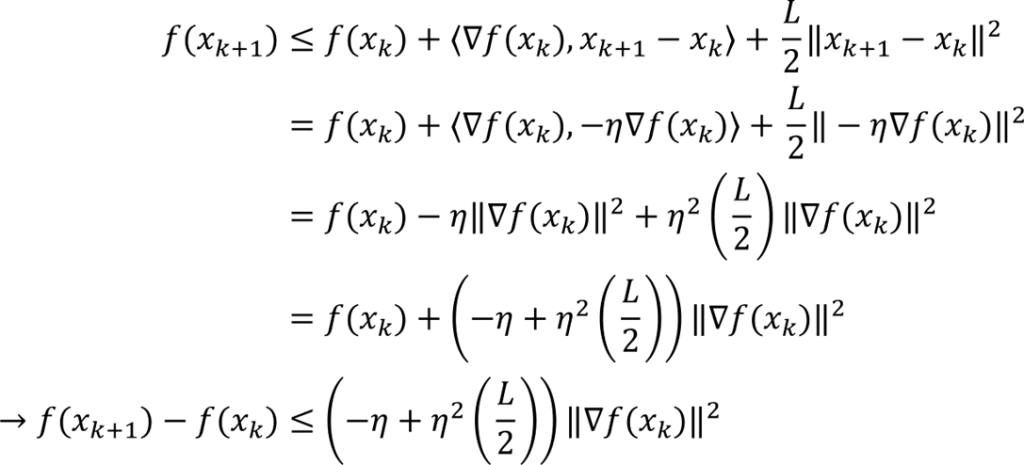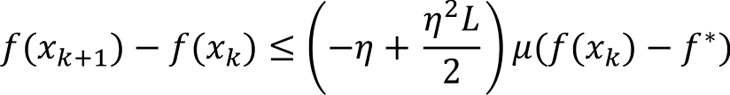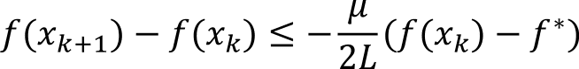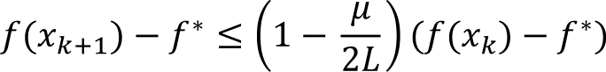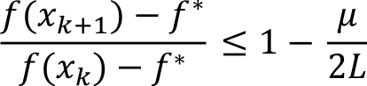Work by Yujin Tang and David Ha

In a paper accepted to the upcoming NeurIPS 2021 conference, researchers at Google Brain created a reinforcement learning (RL) agent that uses a collection of sensory neural networks trained on segments of the observation space and uses an attention mechanism to communicate information between the sensory networks. The interactive demo shows that an agent trained to balance a cartpole (the CartPoleSwingUpHarder environment) can continue to succeed at its task even when the order of the observations is permuted during operation in real time – very impressive! The other videos show similar performance on the PyBullet Ant robot environment and simple videogame environments.

TwoMinutePapers gave an entertaining and concise summary of this work as well.

Allow me to address an important concept in RL that will make the performance of these agents even more remarkable and perhaps surprising. Perhaps the most persistent and onerous concern in data-driven control is robustness to uncertainty. Uncertainties can arise due to inherent time-varying randomness in the environment, as well as (nearly-)static changes in the environment which manifest as distribution shift in data observed by a controller. A standard trick in RL to promote robustness is domain randomization. In this procedure, certain aspects of the environment are changed during training of a control policy. In so doing, the learner is exposed to a wider variety of situations, which are presumed to somehow make the learner “aware” of the potential uncertainties that exist and hence learns a policy that accounts for these uncertainties.

The simplest optimal control task is linear quadratic regulation (LQR), which has been argued as the natural starting point for analysis of learning-based control:

“If a machine learning algorithm does crazy things when restricted to linear models, it’s going to do crazy things on complex nonlinear models too.”

-Ben Recht

Analogously, I argue that multiplicative noise (aka stochastic system parameters) is the simplest type of domain randomization for learning-based control. Our group has extensively studied the properties of linear systems with multiplicative noise in learning-based control, and established both theoretically and empirically that designing (training) controllers in the presence of multiplicative noise does indeed produce robustness of stability to parameter uncertainty.

What is amazing about Google Brain’s permutation-invariant agents is that they achieve permutation-invariance without the need for domain randomization; during training, the order of the observations was kept constant, and only at test time was the observation ordering permuted. In fact, the permutation-invariance is explicitly considered through the design of the attention mechanism, which merges the outputs of the sensory neurons in a permutation-invariant way. This suggests that the need for domain randomization during training can be obviated if the form of the domain uncertainty is known ahead of time and can be designed into the control policy architecture.

I leave the reader with a natural follow-on question:

Is there an analogous way to design a control policy architecture that is robust to system parameter uncertainties without the need for domain randomization during training?

Work by Mathias Lechner, Ramin Hasani, Radu Grosu, Daniela Rus, Thomas A. Henzinger

This paper was recently accepted to ICRA 2021, posted to arXiv, and summarized in this VentureBeat post.

Their research suggests that adversarial training of neural network-based image classifiers, when applied in robot learning settings, can have the opposite of the intended effect, i.e. that adversarially-trained classifiers lead to less safe system operation than their nominal counterparts.

This work highlights the importance in aligning the specification of the adversarial training and the control objective. In particular, they demonstrate that the intuitive low-level training goal of maintaining high image classification accuracy under norm-bounded adversarial perturbations is not sufficient to provide the high-level goal of maintaining high safety of system trajectories under the same adversarial perturbations. This suggests that, to achieve true safety, some type of coupling between high-level control and low-level image classification must be enforced during training.

This work also highlights the large gap between theory and practice in data-driven control. In the literature on statistical learning for linear systems, rigorous guarantees of robustness are typically provided in a classical systems-theoretic sense e.g. ensuring stability of a system subject to model uncertainties and process + measurement disturbances.

For instance, in the CONLab work “Policy Iteration for Linear Quadratic Games with Stochastic Parameters” (IEEE Xplore) (ResearchGate) we consider the setting of a linear system with full-state linear feedback control. We combine stochastic parameters as a device during control design to induce robustness to structured parametric uncertainty, with additive adversarial disturbances to handle unstructured model uncertainty. We also draw an analogy with the machine learning literature, where unstructured uncertainty is addressed by adversarial training examples, while structured uncertainty is addressed by domain randomization.

On the other hand, to control more complicated nonlinear systems, practitioners often use highly expressive neural networks for encoding and approximating value functions and control policies, as well as for processing raw measurements e.g. LiDAR and video image data, whose post-training behavior is not fully understood. Ensuring safety of neural network-based controllers in robot applications may be possible if the control safety can be meaningfully related to the neural network sensitivity using e.g. the Lipschitz constant (e.g. “Efficient and Accurate Estimation of Lipschitz Constants for Deep Neural Networks” arXiv) or constraining predictions to a safety set in the output space (e.g. “Safety Verification and Robustness Analysis of Neural Networks via Quadratic Constraints and Semidefinite Programming” arXiv).

Kudos to the authors Lechner, Hasani, Grosu, Rus, and Henzinger for alerting practitioners to the dangers of naively applying adversarial training in robot learning. We will do our part to bridge the theory practice gap and provide techniques for achieving true safety in data-driven robot operations.

We came across these interesting works that are somewhat tangential to our interests, but fascinating all the same.

Physics in N dimensions

Marc ten Bosch developed a formulation for rigid body dynamics that is independent of the dimension of the space, which is described using geometric algebra. An interesting issue that was also solved was that of collision resolution, which is handled elegantly for convex polytopes which are sufficient to represent typical objects to a high level of accuracy. The paper was accepted to SIGGRAPH 2020 and has been implemented as the commercially available 4D toys as well as an upcoming computer game. Two Minute Papers also covered this game/research.

Reaction-diffusion dynamics

Reaction-diffusion dynamics generalize the diffusion-only dynamics readers may be familiar with from the field of networked systems, which can actually be thought of as a discretization of the diffusion/heat partial differential equation. When the new reaction term is added, rather interesting behavior emerges due to the nonlinearities in the dynamics.

This page shows Robert Munafo’s exploration of different regimes of the parameter space of the reaction-diffusion dynamics.

One particularly interesting setting is called the “U-skate world,” which exhibits emergent patterns somewhat similar to Conway’s Game of Life e.g. the appearance of “still-lifes,” small portions of the state-space that retain their structure over time and “gliders,” small portions of the state-space that both retain their structure over time and move across the state-space by delicate balancing of the forces over their bodies.

SmoothLife

Conway’s Game of Life was a seminal development in computer science that spurred thought about information theory. It was a simple set of rules meant to mimic conditions of population pressures and incentives in living creatures, known as a cellular automata. The game is played on a grid and each cell has a binary state which is updated at discrete time steps. Stephan Rafler generalized the mathematical formulation of this game to continuous state and time, leading to qualitatively similar behavior as Conway’s Game, but with much more organic and arguably richer phenomena, including self-propelled gliders and chain-like structures. Check out the paper, the code, and some YouTube videos. Lex Fridman also interviewed Stephen Wolfram, another giant of computing, wherein they discussed cellular automata.

Inaugural Bode Lecture by Dr. Gunter Stein, CDC, 1989

Keywords: Stability, robustness, fundamental limitations, Bode integral, sensitivity, waterbed effect

Summary

In this classic entertaining lecture delivered by Dr. Gunter Stein, fundamental limitations arising in control pertaining to stability, performance, and robustness are addressed. In particular, the Bode integral is advocated as a fundamental “conservation law” of control, despite its relative obscurity at the time, which arguably persists to this day. Other highlights include demonstrations of the effect of unstable poles both on the ubiquitous simple inverted pendulum, as well as the then-state-of-the-art X-29 aircraft with forward-swept wings; these two systems are more similar than a passing glance would suggest! Dr. Stein’s prescient observations on the twin trends of ever more dangerous systems being controlled and increasing detachment of control theoreticians from these systems, whether due to over-emphasis on formal mathematics or due to automatic “optimal” control synthesis, are perhaps more sobering than ever today in light of recent developments in autonomous driving systems, power networks, and data-driven learning control.

Watch the video here and read the paper here.

Work by Zhangjing Wang, Yu Wu, and Qingqing Niu, IEEE Access Volume: 8, 2020

Keywords: Multi Sensor Fusion, Autonomous Driving, Tracking, Data Association

Summary

The authors present a survey for multi-source and heterogeneous information fusion for autonomous driving vehicles. They discuss three main topics:

1. Sensors and communications: identifying the most popular sensors and communication schemes for autonomous driving and their advantages and disadvantages
2. Fusion: dividing fusion approaches into four main strategies: discernible units, feature complementarity, target attributes of different sensors, and decision making of different sensors.
3. Data association: describing methods for data association for single or multiple sensors detecting spare or multiple targets.

Read the paper on IEEE here.

Work by Dimitris Bertsimas & Ioana Popescu, SIAM Journal on Optimization, Volume: 15, Number: 3, Pages: 780-804, 2005

Keywords: Bounds in Probability Theory , Higher Order Moment Based SDP

Summary

The authors investigate the problem of obtaining best possible bounds on the probability that a certain random variable belongs in a given set, given information on some of its moments (up to kth-order) famously called as the (n, k, Ω)-bound problem. They formulate it as an optimization problem and use modern optimization theory, in particular convex and semidefinite programming. In particular, they provide concrete answers to the following three key questions namely:

1. Are such bounds “best possible”; that is, do there exist distributions that match them?
2. Can such bounds be generalized in multivariate settings, and in what circumstances can they be explicitly and/or algorithmically computed?
3. Is there a general theory based on optimization methods to address in a unified manner moment-inequality problems in probability theory?

Key Observations

• In the univariate case, optimal bounds on P(X ∈ S), when the first k moments of X are given, is given by the solution of a SDP in k + 1 dimensions, where S denotes the set of interest.
• In the multivariate case, if the sets S and Ω are given by polynomial inequalities, an improving sequence of bounds are obtained by solving SDPs of polynomial size in n, for fixed k.
• It is NP-hard to find tight bounds for k ≥ 4 and Ω = Rn and for k ≥ 2 and Ω = Rn+ respectively with rational problem data.
• For k = 1 and Ω = Rn+, it is possible to find tight upper bounds by solving n convex optimization problems when the set S is convex and a polynomial time algorithm is given when S and Ω are unions of convex sets, over which linear functions can be optimized efficiently.
• For k = 2 and Ω = Rn, authors present an algorithm for finding tight bounds when S is a union of convex sets, over which convex quadratic functions can be optimized efficiently.

Possible Applications of Ideas Presented in this Paper

1. Propagating uncertainties in risk-bounded motion planning with the risk of a trajectory being quantified using the probability bounds presented in this paper
2. Anomaly detection in cyber physical systems where higher order moments of a residual data from a state estimator can be used to design anomaly detector thresholds that can satisfy an user prescribed false alarm rate.

Read the paper on SIAM here.

Work by Curtis Madsen, Prashant Vaidyanathan, Sadra Sadraddini, Cristian-Ioan Vasile, Nicholas A. DeLateur, Ron Weiss, Douglas Densmore, and Calin Belta, IEEE CDC 2018

Keywords: Signal Temporal Logic, Metric Spaces

Summary

The authors discuss how STL formulae can admit a metric space under mild assumptions. They present two metrics: the Pompeiu-Hausdorff (PH) and the Symmetric Difference (SD) metrics. The PH distance measures how much the language of one formula needs to be enlarged to include the other. The SD distance measures the overlap between the two formulae. The PH distance can be formulated as a Mixed-Integer Linear Programming (MILP) optimization problem which can be computed fairly quickly (although complexity grows exponentially with the number of predicates are formulae horizon). The SD distance is computed using a recursive algorithm based on the area of satisfaction. Its complexity depends on the complexity of the norm operation.

Read the paper on arXiv here.

Work by Tao Yang, et al., Annual Reviews in Control 2020

Discussion by Yi Guo, February 18, 2020

Keywords: Control review, distributed optimization, algorithm design

Summary

In distributed optimization of multi-agent systems, agents cooperate to minimize a global function which is a sum of local objective functions. Motivated by applications including power systems, sensor networks, smart buildings, and smart manufacturing, various distributed optimization algorithms have been developed. In these algorithms, each agent performs local computation based on its own information and information received from its neighboring agents through the underlying communication network, so that the optimization problem can be solved in a distributed manner.

This survey paper aims to offer a detailed overview of existing distributed optimization algorithms and their applications in power systems. More specifically, the authors first review discrete-time and continuous-time distributed optimization algorithms for undirected graphs. The authors then discuss how to extend these algorithms in various directions to handle more realistic scenarios. Finally, the authors focus on the application of distributed optimization in the optimal coordination of distributed energy resources.

Read the paper on Elsevier here.

Work by Samira S. Farahani, Rupak Majumdar, Vinayak S. Prabhu, and Sadegh Soudjani, IEEE Transactions on Automatic Control August 2019

Keywords: Signal temporal logic, model predictive control, stochastic disturbances

Summary

The authors discuss a shrinking horizon model predictive control (SH-MPC) problem to generate control inputs for a discrete-time linear system under additive stochastic disturbance (either Gaussian or bounded support). The system specifications are through a signal temporal logic (STL) formula and encoded as a chance constraint into the SH-MPC problem. The SH-MPC problem is optimized for minimum input and maximum robustness.

The authors approximate the system robustness in the objective function using min-max and max-min canonical forms of min-max-plus-scaling (MMPS) functions. They under approximate the chance constraint by showing that any chance constraint on a formula can be transformed into chance constraints on atomic propositions, then they transform the latter into linear constraints.

Read the paper on arXiv here or on IEEE Xplore here.

Work by Hamed Karimi, Julie Nutini, and Mark Schmidt, ECML PKDD 2016

Keywords: Nonconvex, optimization, Polyak-Lojasiewicz inequality, gradient domination, convergence, global

Summary

The authors re-explore the Polyak-Lojasiewicz inequality first analyzed by Polyak in 1963 by deriving convergence results under various descent methods for various modern machine learning tasks and establishing equivalences and sufficiency-necessity relationships with several other nonconvex function classes. A highlight of the paper is a beautifully simple proof of linear convergence using gradient descent on PL functions, which we walk through in our discussion.

Read the paper on arXiv here.

Convergence of gradient descent under the Polyak-Lojasiewicz inequality

This proof is extremely short and simple, requiring only a few assumptions and a basic mathematical background. It is strange that it is as universally known as the theory related to convex optimization.

Relating to the theory of Lyapunov stability for nonlinear systems, the PL inequality essentially means that the function value itself is a valid Lyapunov function for exponential stability of the global minimum under the nonlinear gradient descent dynamics.

Lieven Vandenberghe’s lecture notes for the case of strongly convex functions are an excellent supplement.

The setting we consider is that of minimizing a function f(x).

Lipschitz continuity

A function is Lipschitz continuous with constant L if

Likewise the gradient (first derivative) of a function is Lipschitz continuous with constant L if

For the next steps we follow slide 1.13 of Lieven Vandenberghe’s lecture notes.

Recall the Cauchy-Schwarz inequality

Applying the Cauchy-Schwartz inequality to the Lipschitz gradient condition gives

Define the function g(t) as

If the domain of f is convex, then g(t) is well-defined for all t in [0, 1].

Using the definition of g(t), the chain rule of multivariate calculus, and the previous inequality we have

Using the definition of g(t) we can rewrite f(y) in terms of an integral by using the fundamental theorem of calculus

Integrating the second term from 0 to t and using the previous inequality and the derivative of g(t) we obtain

Substituting back into the expression for f(y) we obtain the quadratic upper bound

The Polyak-Lojasiewicz inequality

A function is said to satisfy the Polyak-Lojasiewicz inequality if the following condition holds:

where f* is the minimum function value.

This means that the norm of the gradient grows at least as fast as a quadratic as the function value moves away from the optimal function value.

Additionally, this implies that every stationary point of f(x) is a global minimum.

Gradient descent

The gradient descent update simply takes a step in the direction of the negative gradient:

We are now ready to prove convergence of gradient descent under the PL inequality i.e. Theorem 1 of Karimi et al.

Rearranging the gradient descent update gives the difference

Using the gradient descent update rule in the quadratic upper bound condition (from Lipschitz continuity of the gradient) we obtain

If the stepsize is chosen so that the coefficient on the righthand side is negative, then using the Polyak-Lojasiewicz inequality gives

The range of permissible stepsizes is [0, 2/L] with the best rate achieved with a stepsize of 1/L. Under this choice, we obtain

Adding f(x_k) – f* to both sides gives

Dividing by f(x_k) – f* gives the linear (geometric) convergence rate

This shows that the difference between the current function value and the minimum decreases at least as fast as a geometric series with a rate determined by the ratio of the PL and Lipschitz constants.

Why would control systems researchers care about this?

The Polyak-Lojasiewicz inequality is key to analysis of convergence of policy gradient for LQR and LQR with multiplicative noise.