Benjamin Gravell, Peyman Mohajerin Esfahani, Tyler Summers, IEEE Transactions on Automatic Control (TAC) 2020
Keywords: Optimal, robust, control, reinforcement learning, policy, gradient, optimization, nonconvex, gradient domination, Polyak-Lojasiewicz, inequality, concentration, bound
Summary
We show that the linear quadratic regulator with multiplicative noise (LQRm) objective is gradient dominated, and thus applying policy gradient results in global convergence to the globally optimum control policy with polynomial dependence on problem parameters. The learned policy accounts for inherent parametric uncertainty in system dynamics and thus improves stability robustness. Results are provided both in the model-known and model-unknown settings where samples of system trajectories are used to estimate policy gradients.
Read the paper on IEEE Xplore or arXiv.
Overview
Policy gradient is a general algorithm from reinforcement learning; see Ben Recht’s gentle introduction. At a high level, it is simply the application of (stochastic) gradient descent to the parameters of a parametric control policy. Although traditional reinforcement learning treats the tabular setting with discrete state and action spaces, most real-world control problems deal with systems that have continuous state and action spaces. Luckily, policy gradient works much the same way in this setting.
In this post we walk through some of the key points from our paper; see the full text for more details and variable definitions.
Setting: LQR with multiplicative noise
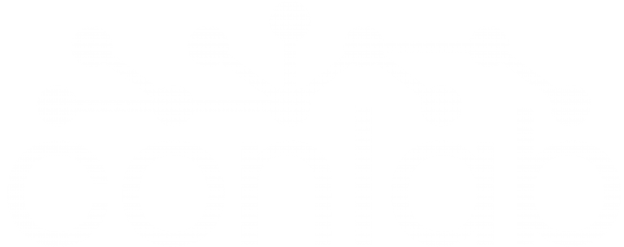
We consider the following infinite-horizon stochastic optimal control problem with an objective quadratic in the state and input with stochastic dynamics with multiplicative noises (LQRm problem). Expectation is with respect to the initial state and the multiplicative noise.
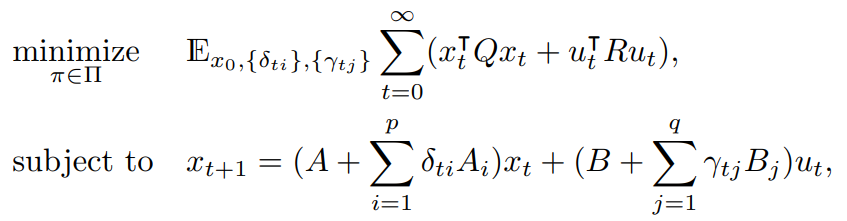
Any solution to this problem must be stabilizing, however in the context of stochastic systems we must deal with a stronger form of stability known as mean-square stability which requires not only that the expected state return to the origin over time, but also that the (auto)covariance of the state decrease to zero over time:
Mean-square stability:
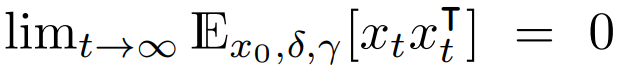
Mean-square stability can be further characterized in terms of the vectorized state covariance dynamics operator
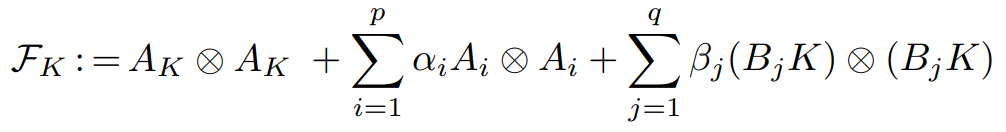

The LQRm problem is special since it, like the deterministic LQR problem, admits a simple solution which is computable from a Riccati equation, specifically this one:
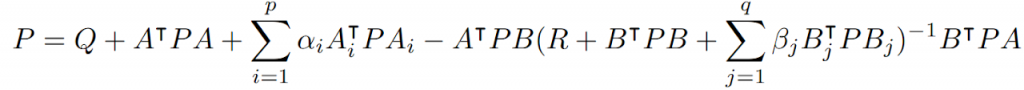
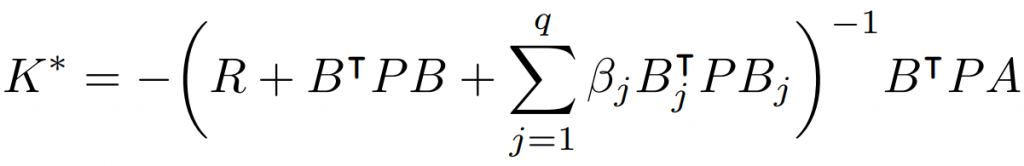
However, unlike the LQR problem with additive noise, the multiplicative noises change the optimal gain matrix relative to the deterministic case. In particular, the multiplicative noise can be used as a proxy for uncertainty in the model parameters of a deterministic linear model.
Motivation: robust stability
A key issue in control design is robustness i.e. ensuring stability in the presence of model parameter uncertainty. The following example motivates how stochastic multiplicative noise ensures deterministic robustness.

Although this is a simple example, it demonstrates that the robustness margin increases monotonically with the multiplicative noise variance. We also see that when α = 0 the bound collapses so that no robustness is guaranteed, i.e., when |a| → 1. This result can be extended to multiple states, inputs, and noise directions, but the resulting conditions become considerably more complex.
Case of known dynamics
We already saw that we can solve the optimal control problem exactly (up to a Riccati equation), so what else is there to study? We ultimately care about the case when dynamics are unknown (e.g. as in adaptive control or system identification) which can be handled by policy gradient.
To begin we see how policy gradient works when the dynamics are fully known, in which case the policy gradient can be evaluated analytically in terms of the dynamics:

With this expression, we can prove the key result that the LQRm objective is gradient dominated in the control gain matrix K:
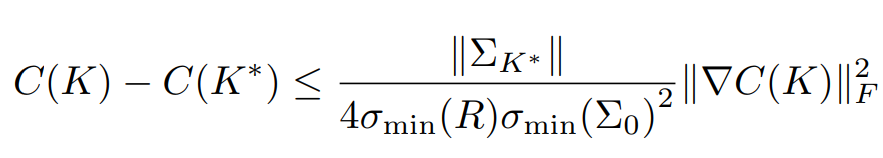
This (along with Lipschitz continuity) immediately implies that (policy) gradient descent with an appropriate constant step size will converge to the global minimum, i.e. the same solution found by solving a Riccati equation, at a linear (geometric) rate from any initial point. For those familiar with convex optimization, gradient domination bears some similarities to the more restrictive strong convexity condition, which essentially puts a lower bound on the curvature of the function, thus ensuring gradient descent makes sufficient progress at each step anywhere on the function. See Theorem 1 of this paper for an extremely short proof of convergence under the gradient domination (Polyak-Lojasiewicz) condition.
The bulk of the technical work that follows goes towards bounding the Lipschitz constant, and thus the step size and convergence rate. We also analyze the natural policy gradient and “Gauss-Newton” steps in parallel to Fazel et al. – these steps give faster convergence than vanilla policy gradient but require more information. Note that “Gauss-Newton” step with a stepsize of 1/2 is exactly the policy iteration algorithm (another model-free RL technique) first proven to converge for standard LQR in the case of known dynamics in continuous-time by Kleinman in 1968 and in discrete-time by Hewer in 1971 and in the case of unknown dynamics by Bradtke, Ydstie, and Barto at the 1994 ACC. Note that many authors from the 1960s and 1970s did not frame their results under the modern dynamic programming/reinforcement learning labels of “policy iteration” or “Q-learning” but rather as iterative solutions of Riccati equations.
Case of unknown dynamics
When the dynamics are unknown, the (policy) gradient must be obtained empirically via estimation from sample trajectories. We use the following algorithm to do this:

In this case, we use tools from high-dimensional statistics known as concentration bounds to ensure that with high probability the error between the estimated and true gradients is smaller than a threshold. The threshold is chosen small enough that gradient descent with the same step size as in the case of exact gradients provably converges.
Numerical experiments
We validated policy gradient in the case of known dynamics – this is much faster to simulate than the case of unknown dynamics due to the large number of samples required to estimate the policy gradient accurately.
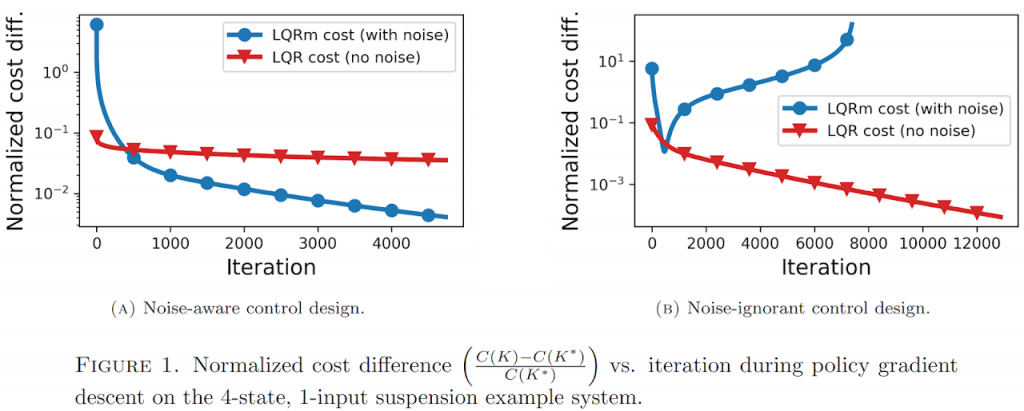
The first example shows policy gradient working on a suspension system with 2 masses (4 states) and a single input. To demonstrate the peril of failing to account for multiplicative noise when it truly exists, we ran policy gradient both (a) accounting for and (b) ignoring the multiplicative noise. The blue curves show the control evaluated on the LQR cost with multiplicative noise while the red curves show the control evaluated on the LQR cost without multiplicative noise. When the noise is ignored, the control destabilized the truly noisy system in mean-square. When noise is assumed, the control achieves lower performance on the truly noiseless system, but does not and cannot destabilize it.
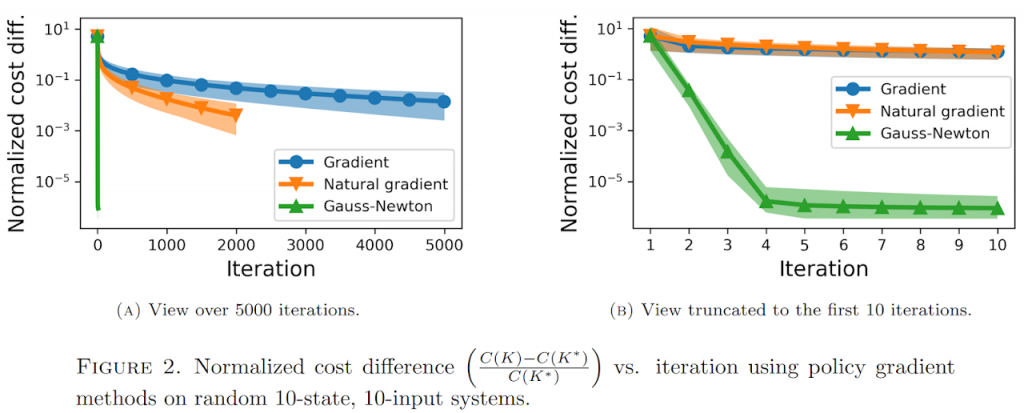
The second example shows policy gradient and its faster cousins applied on a random 10-state, 10-input system. With more iterations, the global optimum is more closely approximated.
Opinions & take-aways
Although the techniques used in this work and Fazel et al. represent a novel synthesis of tools from various mathematical fields, simpler/shorter proofs would help reduce barriers-to-entry for controls researchers unfamiliar with the finer points of reinforcement learning and statistics.
Convergence results were shown, but sample efficiency is still a major concern. Model-based techniques have been shown to be significantly more efficient for learning to control linear systems. This is somewhat expected since a linear dynamics model is the simplest possible; model-free techniques may be competitive when the dynamics are highly nonlinear and difficult to model based solely on data.
Related work
We envision multiplicative noise as a modeling framework for ensuring robustness; see older work from Bernstein which informs this notion. Perhaps the best known framework for robustness in multivariate state space control is H-infinity control. Applying policy gradient to the dynamic game formulation of this framework has received attention lately as well; see positive results in the two-player setting and negative results in the many-player setting.