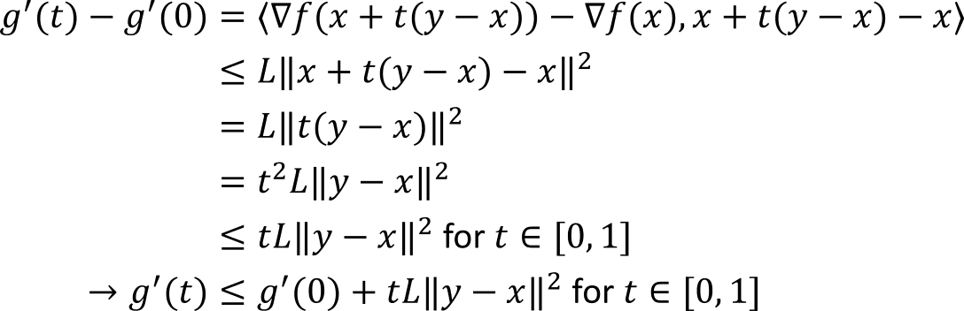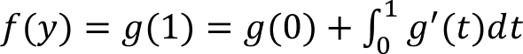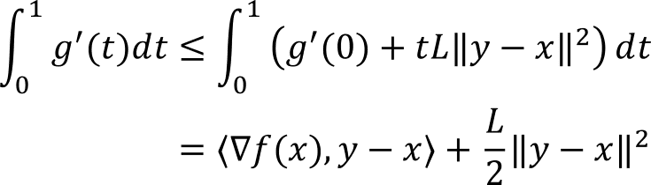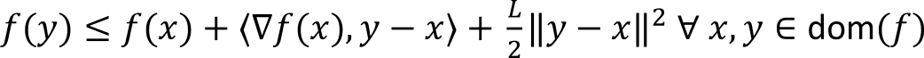Work by Dimitris Bertsimas & Ioana Popescu, SIAM Journal on Optimization, Volume: 15, Number: 3, Pages: 780-804, 2005
Keywords: Bounds in Probability Theory , Higher Order Moment Based SDP
Summary
The authors investigate the problem of obtaining best possible bounds on the probability that a certain random variable belongs in a given set, given information on some of its moments (up to kth-order) famously called as the (n, k, Ω)-bound problem. They formulate it as an optimization problem and use modern optimization theory, in particular convex and semidefinite programming. In particular, they provide concrete answers to the following three key questions namely:
- Are such bounds “best possible”; that is, do there exist distributions that match them?
- Can such bounds be generalized in multivariate settings, and in what circumstances can they be explicitly and/or algorithmically computed?
- Is there a general theory based on optimization methods to address in a unified manner moment-inequality problems in probability theory?
Key Observations
- In the univariate case, optimal bounds on P(X ∈ S), when the first k moments of X are given, is given by the solution of a SDP in k + 1 dimensions, where S denotes the set of interest.
- In the multivariate case, if the sets S and Ω are given by polynomial inequalities, an improving sequence of bounds are obtained by solving SDPs of polynomial size in n, for fixed k.
- It is NP-hard to find tight bounds for k ≥ 4 and Ω = Rn and for k ≥ 2 and Ω = Rn+ respectively with rational problem data.
- For k = 1 and Ω = Rn+, it is possible to find tight upper bounds by solving n convex optimization problems when the set S is convex and a polynomial time algorithm is given when S and Ω are unions of convex sets, over which linear functions can be optimized efficiently.
- For k = 2 and Ω = Rn, authors present an algorithm for finding tight bounds when S is a union of convex sets, over which convex quadratic functions can be optimized efficiently.
Possible Applications of Ideas Presented in this Paper
- Propagating uncertainties in risk-bounded motion planning with the risk of a trajectory being quantified using the probability bounds presented in this paper
- Anomaly detection in cyber physical systems where higher order moments of a residual data from a state estimator can be used to design anomaly detector thresholds that can satisfy an user prescribed false alarm rate.
Read the paper on SIAM here.