Sleiman Safaoui, Lars Lindemann, Iman Shames, Tyler H Summers, ACC 2022.
Keywords: Risk-based control, stochastic systems, Temporal Logic
Overview
In a previous work, we studied the problem of designing discrete-time risk-bounded controls for linear systems with temporal logic specifications.
- Temporal logic specifications define spatial and temporal constraints to be enforced.
- Examples of spatial constraints: avoid sets (collision regions), goal regions, …
- Examples of temporal constraints: setting a time limit on reaching a region (reach the goal in at most 10 time-steps) or specifying an order for visiting regions.
- Risk-bounded controls are controls that result in the system satisfying the constraints with a certain probability guarantee.
- Instead of simply assuming a Gaussian distribution, we consider a set of distributions that includes all distributions that have certain features (also called an ambiguity set).
- The ambiguity set we consider is the moment-based ambiguity set: the set of all distributions with specific mean and covariance (or first two moments).
In this work, we consider the continuous-time analog of our previous work; i.e. we are interested in generating control commands that would render a continuous-time systems safe and enable it of satisfying its spatial and temporal requirements. Similarly, we consider stochastic linear systems affected by additive noise whose distribution belongs to the moment-based ambiguity set.
The continuous-time problem is more difficult.
- Instead of having discrete control values to optimize over, we have to deal with stochastic integrals. But, stochastic integrals are mostly studied in the case of Gaussian noise. Thus, handling non-Gaussian cases is to some extent novel.
- Finding an open-loop control over a horizon requires solving a constrained continuous-time optimization problem. Continuous-time optimal control is difficult itself (requires using Pontryagin’s maximum principle or solving the Hamilton-Jacobi-Bellman equation). In our problem we also have time-varying constraints.
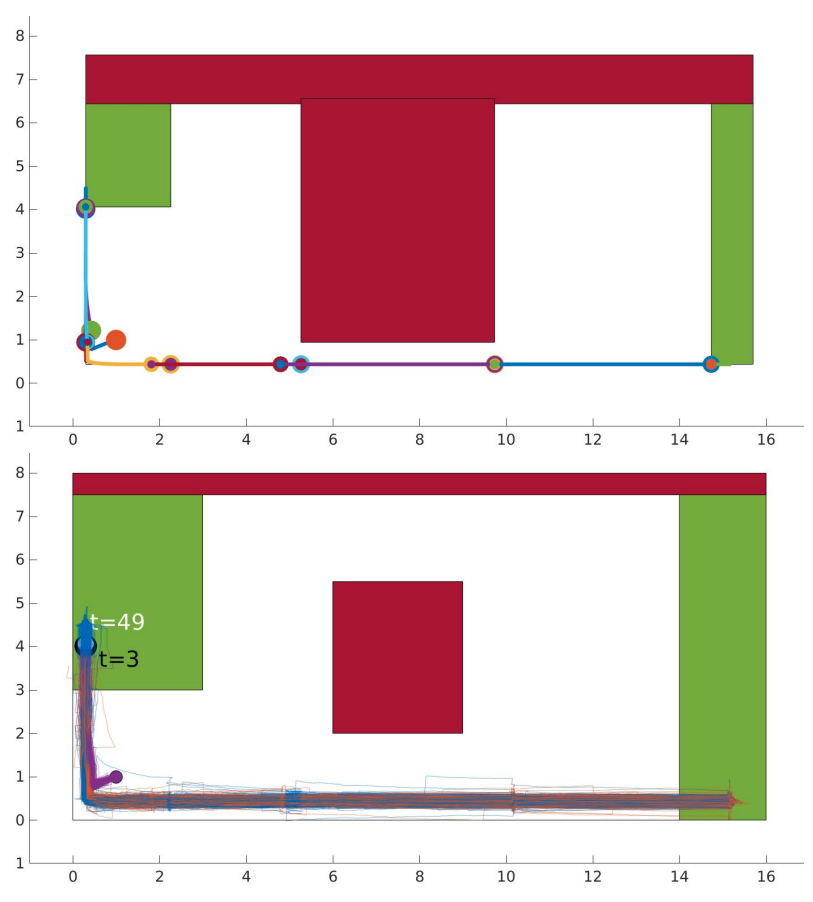
Bottom: actual constraints.
Robot avoids red regions (top and center) and has to alternate between visiting the left and right green regions
In our work, we provide a sufficient solution to the problem that consists of:
- using timed-signal transducers to divide the environment into adjacent convex regions
- reformulating the dynamics to obtain deterministic risk-tightened dynamics
- formulating a timed-transition continuous-time constrained problem and solving it by discretizing it while tightening our constraints to retain continuous-time guarantees
- and finally stringing together solutions to the sequence of timed-transition problems.
Check out our paper on IEEE Xplore or arXiv!