Sleiman Safaoui*, Benjamin Gravell*, Venkatraman Renganathan*, Tyler H Summers, IEEE/RSJ IROS 2020, submitted.
Keywords: Risk-based planning, stochastic systems, nonlinear systems, RRT
Summary
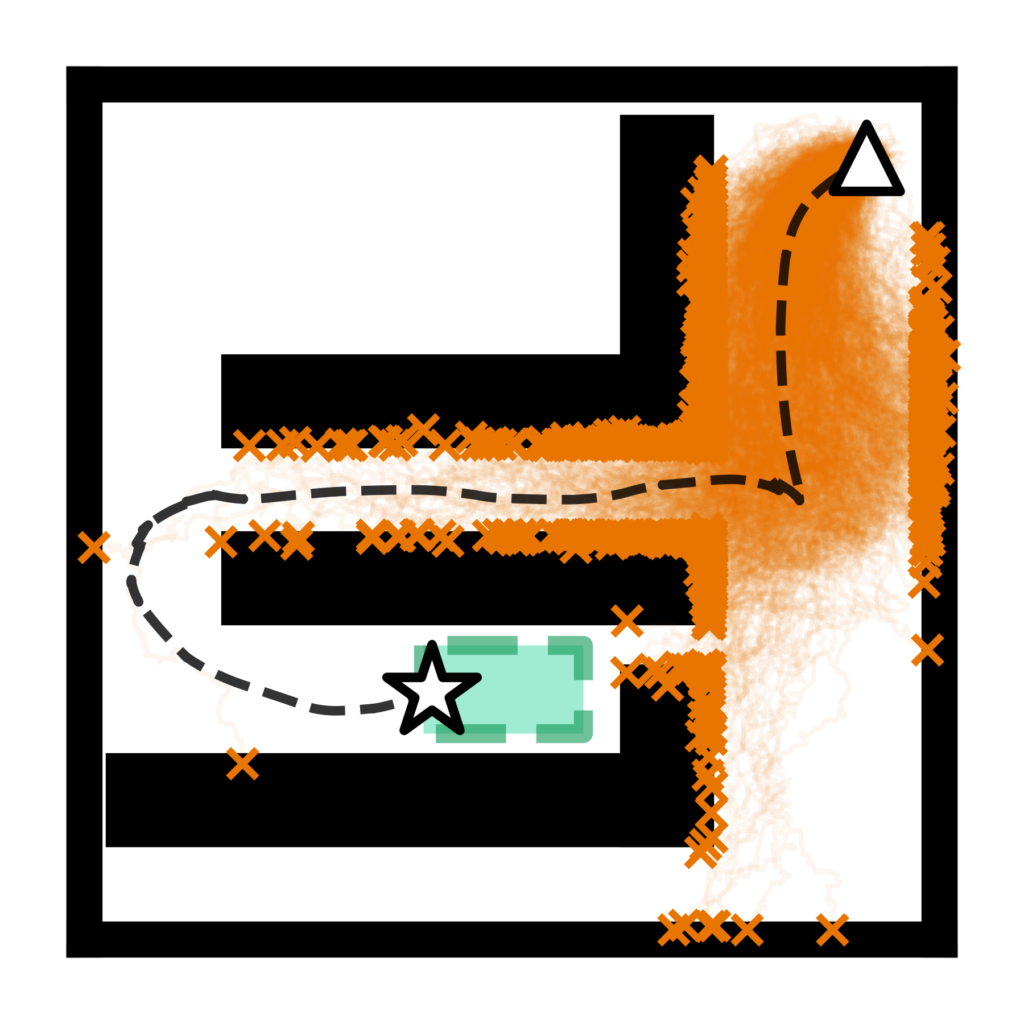
We propose a two-phase risk-averse architecture for controlling stochastic nonlinear robotic systems. RRT* is a high-level sampling-based planning algorithm that is appealing thanks to its asymptotic guarantees of completeness (if a solution exists, it will be found as the number of samples goes to infinity) and optimal (the solution will converge to the optimal value as the number of samples goes to infinity). However, such planners generally do not account for uncertainties while planning resulting in optimistic plans that are prone to failure under uncertainties. Notice how the figure on the left shows an RRT* tree that plans the robot trajectory from the triangle in the upper right corner to the green dashed rectangle passing through the narrow gap to the right of the obstacle. In pursuit of optimality, the plan gets dangerously close to the obstacles (black rectangles). To counter that, we present RANS-RRT*: Risk-Averse Nonlinear Steering RRT*, as an RRT* variant designed for nonlinear dynamics (solves a nonlinear program to steer between nodes) that accounts for risk by approximating the state distribution and applying a distributionally robust collision check to promote safe planning. The figure on the right depicts safety ellipses (yellow circles) at each node that must not collide with the obstacles. Notice how the plan thus avoids the aforementioned gap since it is deemed risky and instead approaches the goal region from the left side.

RRT* 
RANS-RRT*
Having generated a risk-averse plan, the robot uses a low-level controller to track it. We compare three feedback controllers: linear quadratic regulator (LQR), LQR with robustness-promoting multiplicative noise terms (LQRm), and nonlinear model predictive control (NMPC) and the open-loop controller demonstrating the effectiveness of the the feedback controllers, and specifically the chosen NMPC tracker, under heavy-tailed Laplace process noise.
OL 
LQR 
LQRm 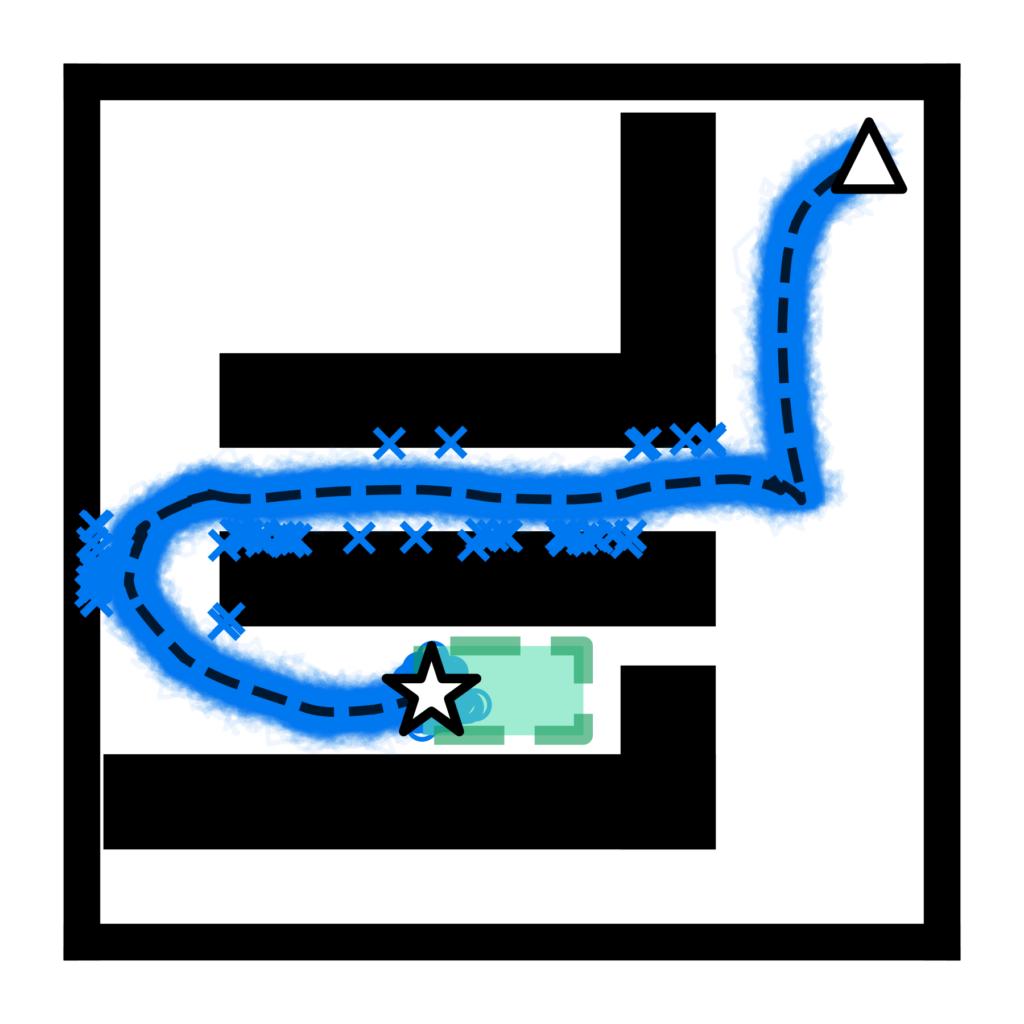
NMPC
We vary the size of the noise covariance from 0.0000005 to 0.1 and count the number of failures due to collisions out the 1000 Monte Carlo trials for each noise level. The results reveal NMPC’s superiority in tracking the trajectory more safely.
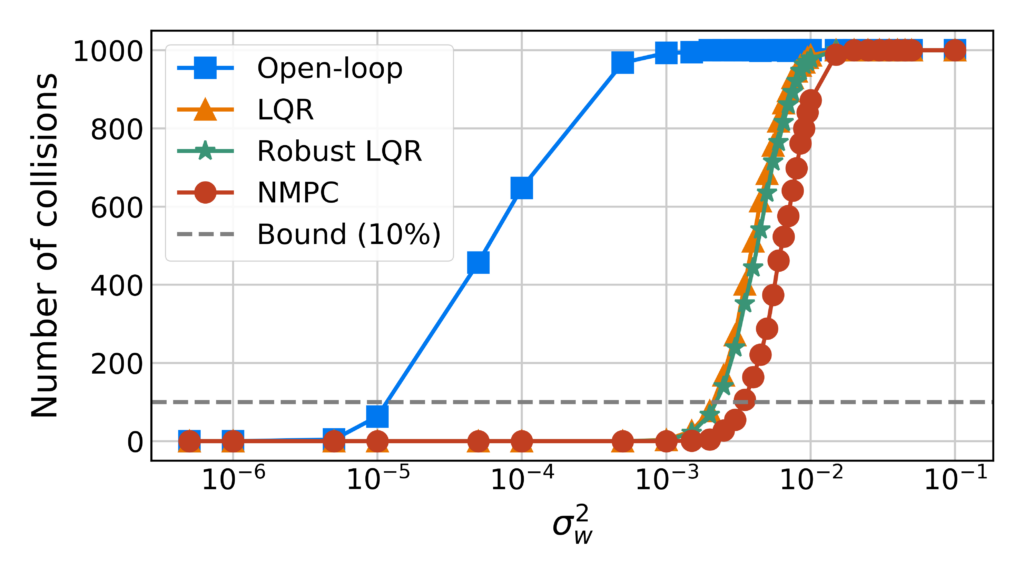
Number of collisions 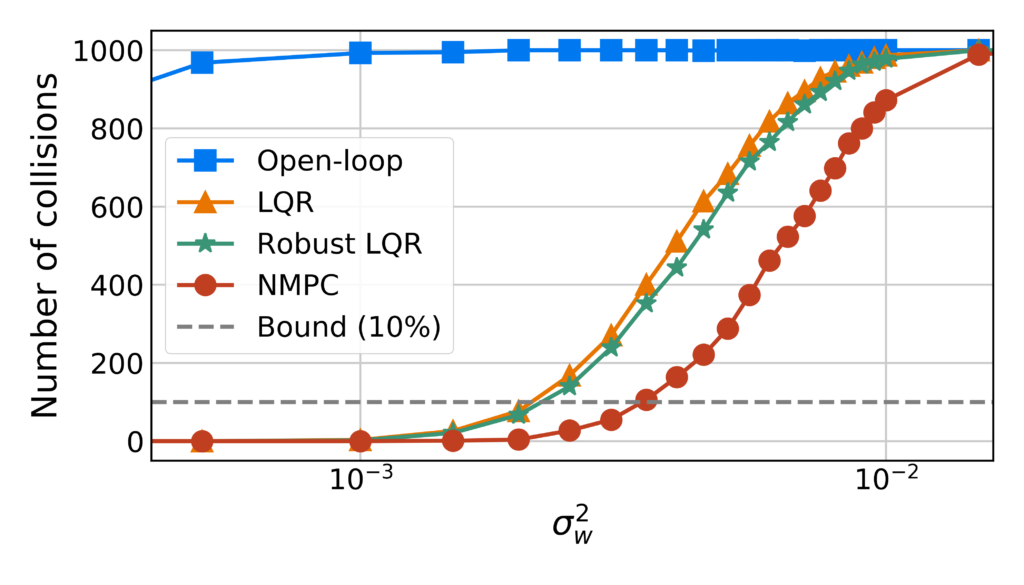
Zoomed View
Read on arXiv.